how to find horizontal asymptotes of rational functions

While vertical asymptotes draw the beliefs of a graph as the output gets very large or very small, horizontal asymptotes aid describe the behavior of a graph as the input gets very large or very small-scale. Call back that a polynomial'due south terminate behavior will mirror that of the leading term. As well, a rational office's terminate behavior volition mirror that of the ratio of the leading terms of the numerator and denominator functions.

There are three singled-out outcomes when checking for horizontal asymptotes:

Case i: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at y= 0.

[latex]\text{Example: }f\left(x\right)=\frac{4x+ii}{{x}^{ii}+4x - 5}[/latex]

In this case, the finish beliefs is [latex]f\left(x\correct)\approx \frac{4x}{{x}^{2}}=\frac{4}{x}[/latex]. This tells usa that, as the inputs increase or decrease without bound, this role volition conduct similarly to the function [latex]g\left(x\right)=\frac{iv}{x}[/latex], and the outputs will approach cipher, resulting in a horizontal asymptote at y= 0. Note that this graph crosses the horizontal asymptote.

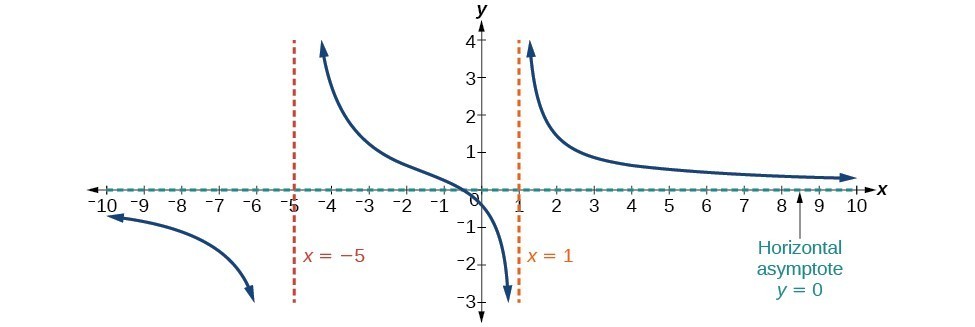
Effigy 12.Horizontal Asymptote y = 0 when [latex]f\left(10\right)=\frac{p\left(x\right)}{q\left(ten\right)}, q\left(x\right)\ne{0}\text{ where degree of }p<\text{degree of }q[/latex].

Example 2: If the degree of the denominator < degree of the numerator by one, we get a camber asymptote.

[latex]\text{Example: }f\left(x\right)=\frac{iii{x}^{two}-2x+1}{ten - 1}[/latex]

In this case, the terminate behavior is [latex]f\left(10\correct)\approx \frac{3{x}^{2}}{ten}=3x[/latex]. This tells u.s.a. that equally the inputs increase or decrease without spring, this role will behave similarly to the part [latex]1000\left(ten\correct)=3x[/latex]. As the inputs abound large, the outputs will abound and not level off, so this graph has no horizontal asymptote. However, the graph of [latex]grand\left(x\right)=3x[/latex] looks like a diagonal line, and since f will deport similarly to yard, it volition approach a line close to [latex]y=3x[/latex]. This line is a slant asymptote.

To find the equation of the slant asymptote, separate [latex]\frac{3{x}^{ii}-2x+one}{x - one}[/latex]. The quotient is [latex]3x+i[/latex], and the rest is two. The camber asymptote is the graph of the line [latex]thousand\left(x\correct)=3x+1[/latex].

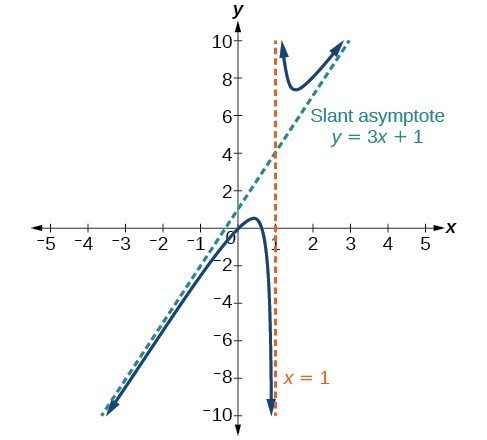
Figure thirteen.Slant Asymptote when [latex]f\left(x\correct)=\frac{p\left(ten\right)}{q\left(ten\right)},q\left(x\right)\ne 0[/latex] where degree of [latex]p>\text{caste of }q\text{ by }1[/latex].

Case 3: If the degree of the denominator = degree of the numerator, in that location is a horizontal asymptote at [latex]y=\frac{{a}_{north}}{{b}_{n}}[/latex], where [latex]{a}_{n}[/latex] and [latex]{b}_{n}[/latex] are the leading coefficients of [latex]p\left(x\correct)[/latex] and [latex]q\left(x\correct)[/latex] for [latex]f\left(x\correct)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0[/latex].

[latex]\text{Case: }f\left(x\right)=\frac{3{x}^{two}+two}{{x}^{ii}+4x - 5}[/latex]

In this example, the end behavior is [latex]f\left(x\right)\approx \frac{iii{ten}^{2}}{{x}^{2}}=3[/latex]. This tells the states that as the inputs grow big, this part will bear like the function [latex]g\left(x\correct)=3[/latex], which is a horizontal line. As [latex]x\to\pm\infty ,f\left(x\right)\to 3[/latex], resulting in a horizontal asymptote at y = 3. Note that this graph crosses the horizontal asymptote.

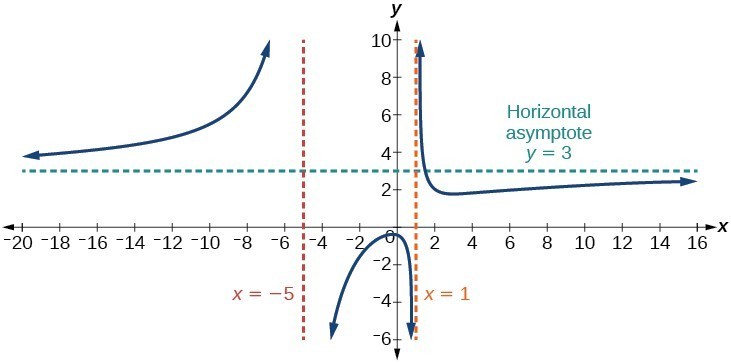
Figure 14.Horizontal Asymptote when [latex]f\left(ten\correct)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0\text{ where caste of }p=\text{degree of }q[/latex].

Detect that, while the graph of a rational office will never cross a vertical asymptote, the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may take many vertical asymptotes, the graph will have at near one horizontal (or camber) asymptote.

Information technology should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end beliefs of the graph volition mimic the behavior of the reduced cease behavior \fraction. For instance, if nosotros had the office

[latex]f\left(10\right)=\frac{3{x}^{v}-{x}^{2}}{x+3}[/latex]

with cease behavior

[latex]f\left(ten\right)\approx \frac{iii{ten}^{5}}{x}=3{x}^{iv}[/latex],

the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.

[latex]x\to \pm \infty , f\left(x\right)\to \infty [/latex]

A Full general Annotation: Horizontal Asymptotes of Rational Functions

The horizontal asymptote of a rational office can exist determined by looking at the degrees of the numerator and denominator.

• Degree of numerator is less than degree of denominator: horizontal asymptote at y= 0.
• Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; camber asymptote.
• Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.

Example 7: Identifying Horizontal and Slant Asymptotes

For the functions below, place the horizontal or slant asymptote.

1. [latex]g\left(x\right)=\frac{vi{10}^{3}-10x}{2{x}^{3}+5{10}^{2}}[/latex]
2. [latex]h\left(10\right)=\frac{{x}^{2}-4x+1}{10+two}[/latex]
3. [latex]k\left(x\right)=\frac{{x}^{2}+4x}{{x}^{three}-8}[/latex]

Solution

For these solutions, we will utilize [latex]f\left(ten\right)=\frac{p\left(x\right)}{q\left(x\right)}, q\left(x\right)\ne 0[/latex].

1. [latex]thou\left(ten\correct)=\frac{6{ten}^{3}-10x}{ii{x}^{3}+five{x}^{2}}[/latex]: The degree of [latex]p=\text{degree of } q=3[/latex], so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at [latex]y=\frac{6}{2}[/latex] or [latex]y=iii[/latex].
2. [latex]h\left(x\correct)=\frac{{x}^{ii}-4x+ane}{10+ii}[/latex]: The degree of [latex]p=2[/latex] and caste of [latex]q=1[/latex]. Since [latex]p>q[/latex] by 1, there is a slant asymptote found at [latex]\frac{{x}^{2}-4x+1}{10+2}[/latex].

   

   The caliber is [latex]x - 6[/latex] and the remainder is thirteen. There is a slant asymptote at [latex]y=x - 6[/latex].

3. [latex]one thousand\left(ten\correct)=\frac{{ten}^{2}+4x}{{10}^{3}-eight}[/latex]: The degree of [latex]p=2\text{ }<[/latex] degree of [latex]q=3[/latex], so there is a horizontal asymptote y = 0.

Instance 8: Identifying Horizontal Asymptotes

In the sugar concentration problem earlier, we created the equation [latex]C\left(t\correct)=\frac{5+t}{100+10t}[/latex].

Discover the horizontal asymptote and interpret information technology in context of the trouble.

Solution

Both the numerator and denominator are linear (degree 1). Because the degrees are equal, there volition be a horizontal asymptote at the ratio of the leading coefficients. In the numerator, the leading term is t, with coefficient i. In the denominator, the leading term is 10t, with coefficient x. The horizontal asymptote will be at the ratio of these values:

[latex]t\to \infty , C\left(t\right)\to \frac{ane}{10}[/latex]

This office will have a horizontal asymptote at [latex]y=\frac{ane}{10}[/latex].

This tells united states of america that every bit the values of t increment, the values of C will approach [latex]\frac{1}{x}[/latex]. In context, this means that, as more time goes by, the concentration of saccharide in the tank will arroyo i-10th of a pound of sugar per gallon of water or [latex]\frac{one}{10}[/latex] pounds per gallon.

Example ix: Identifying Horizontal and Vertical Asymptotes

Find the horizontal and vertical asymptotes of the function

[latex]f\left(x\correct)=\frac{\left(10 - ii\right)\left(x+3\right)}{\left(x - i\right)\left(10+2\correct)\left(ten - 5\right)}[/latex]

Solution

First, annotation that this function has no mutual factors, and then there are no potential removable discontinuities.

The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. The denominator will be goose egg at [latex]x=1,-2,\text{and }5[/latex], indicating vertical asymptotes at these values.

The numerator has degree two, while the denominator has degree 3. Since the caste of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards nothing as the inputs go large, and and then as [latex]x\to \pm \infty , f\left(x\right)\to 0[/latex]. This function will have a horizontal asymptote at [latex]y=0[/latex].

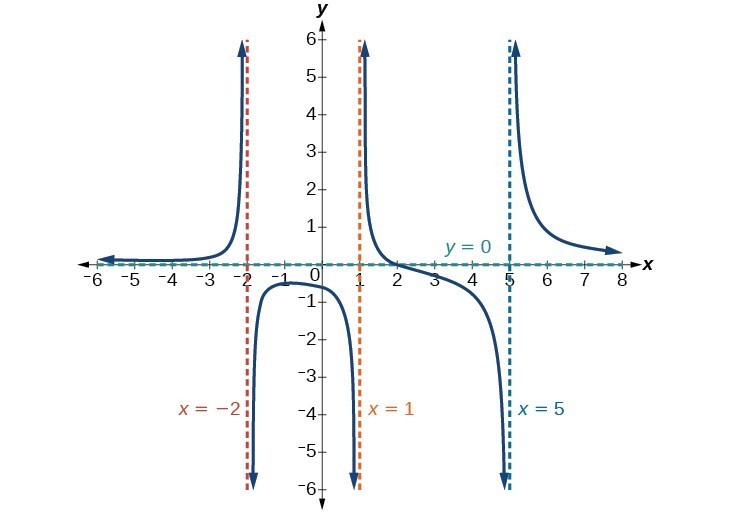
Figure xv

Effort Information technology 6

Find the vertical and horizontal asymptotes of the role:

[latex]f\left(x\right)=\frac{\left(2x - ane\right)\left(2x+1\correct)}{\left(x - 2\correct)\left(x+3\correct)}[/latex]

Solution

A General Note: Intercepts of Rational Functions

A rational role will accept a y-intercept when the input is zero, if the role is defined at zilch. A rational function volition non have a y-intercept if the function is not defined at nothing.

Likewise, a rational function will have x-intercepts at the inputs that crusade the output to exist naught. Since a \fraction is only equal to nix when the numerator is nothing, x-intercepts can simply occur when the numerator of the rational role is equal to zero.

Example 10: Finding the Intercepts of a Rational Office

Find the intercepts of [latex]f\left(x\right)=\frac{\left(x - 2\correct)\left(x+3\right)}{\left(x - 1\right)\left(x+2\right)\left(x - five\right)}[/latex].

Solution

We can find the y-intercept past evaluating the office at zero

[latex]f\left(0\correct)=\frac{\left(0 - 2\correct)\left(0+3\right)}{\left(0 - 1\right)\left(0+2\right)\left(0 - 5\right)}\text{ }=\frac{-six}{10}\text{ }=-\frac{3}{v}\text{ }=-0.half-dozen[/latex]

The x-intercepts volition occur when the function is equal to zero:

[latex]0=\frac{(x-two)(x+3)}{(ten-1)(x+2)(x-5)}[/latex]   This is zero when the numerator is zippo.

[latex]0=(x-2)(x+three)[/latex]

[latex]x=two, -three[/latex]

The y-intercept is [latex]\left(0,-0.half dozen\right)[/latex], the ten-intercepts are [latex]\left(2,0\right)[/latex] and [latex]\left(-3,0\right)[/latex].

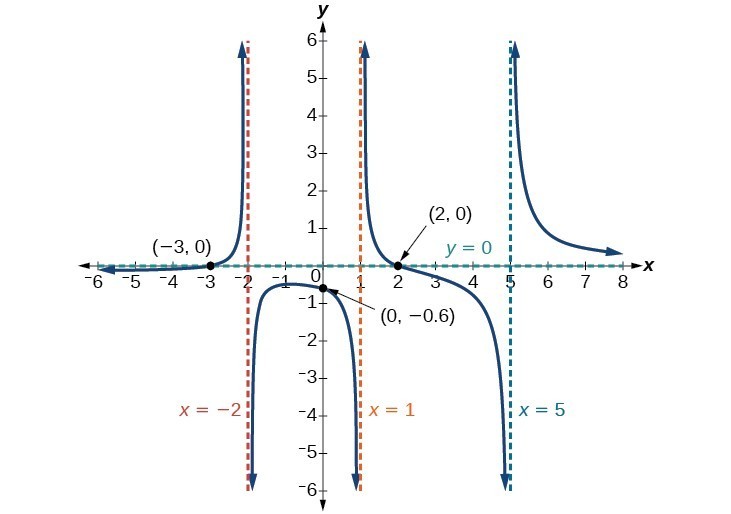
Figure 16

Try It 7

Given the reciprocal squared office that is shifted \right 3 units and downwardly four units, write this as a rational function. And then, observe the ten– and y-intercepts and the horizontal and vertical asymptotes.

Solution

Source: https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/identify-horizontal-asymptotes/

Posted by: slaytonopeashom.blogspot.com

Share this post